Naive Bayes

Overview

Naive Bayes is a supervised learning application that utilizes Bayes' theorem, which assumes that features are conditionally independent. In general, Naive Bayes can be used to construct classifiers. Some useful, practical applications of Naive Bayes: text classification - for instance, determining the sentiment of a document based on the probability of word associations, or predicting if an email is considered legitimate or spam. Based on the simplicity of the mathematics, the algorithm scales very well to large datasets.

Gaussian Naive Bayes implements the naive Bayes algorithm for Gaussian distributed data. The Gaussian Naive Bayes is calculated using the probability of the features given the class, then compares probabilities to determine the prediction. The algorithm is as follows: $$P(x_i\mid y)=\frac{1}{\sqrt{2\pi {\sigma }_y^2}}\exp (-\frac{(x_i-{\mu }_y{)}^2}{2{\sigma }_y^2})$$ The parameters ${\sigma }_y$ and ${\mu }_y$ are estimated using the maximum likelihood estimation. In our application of Gaussian naive bayes, we will utilize the standard scaler to normalize the data.

Multinomial Naive Bayes implements the naive Bayes algorithm for multinomially distributed data. It is typically used for discrete values, such as frequency counts. The algorithm is as follows: $${\hat{\theta }}_{yi}=\frac{N_{yi}+\alpha }{N_y+\alpha n}$$ where $N_{yi}=\sum _{x\in T}{x}_i$ is the number of times feature $i$ appears in a sample of class $y$ in the training set $T$, and $N_y=\sum _{i=1}^n{N}_{yi}$ is the total count of all features for class $y$. It is important to add a smoothing parameter $\alpha \ge 0$ to avoid zero probabilities. In other words, this adds a "ghost" count to account for features not in the training set. Setting $\alpha =1$ is called Laplace smoothing, while setting $\alpha <1$ is called Lidstone smoothing. In our application of multinomial naive bayes, we will utilize binning to convert the data into discrete values.

Bernoulli Naive Bayes implements the naive Bayes algorithm for Bernoulli distributed data. It is typically used for binary values, such as true or false. The algorithm is as follows: $$P(x_i\mid y)=P(x_i=1\mid y)x_i+(1-P(x_i=1\mid y))(1-x_i)$$ One key difference between Bernoulli naive bayes and Multinomial naive bayes is that Bernoulli naive bayes explicitly penalizes the non-occurrence of a feature. In our application of Bernoulli naive bayes, we will utilize one hot encoder to convert the data into a binary matrix, where each column represents a unique value in the dataset.

Categorical Naive Bayes implements the naive Bayes algorithm for categorical distributed data. It is typically used for categorical values, such as nominal values. In our application of Categorical naive bayes, we will utilize one hot encoder to convert the data into a binary matrix, where each column represents a unique value in the dataset.

Smoothing

In general, smoothing is required on the Multinomial and Categorical Naive Bayes algorithms, as these deal with discrete values. Without smoothing, results may lead to zero probabilities, which could hurt model performance. Smoothing may be optional for applications of Bernoulli and Gaussian Naive Bayes, since Bernoulli utilizes binary features (which can be handled in the preprocessing steps), and since Gaussian utilizies continuous values. It may still be good practice to add smoothing to all four algorithms, though, to prevent the occurrence of zero probabilities overall.

Results

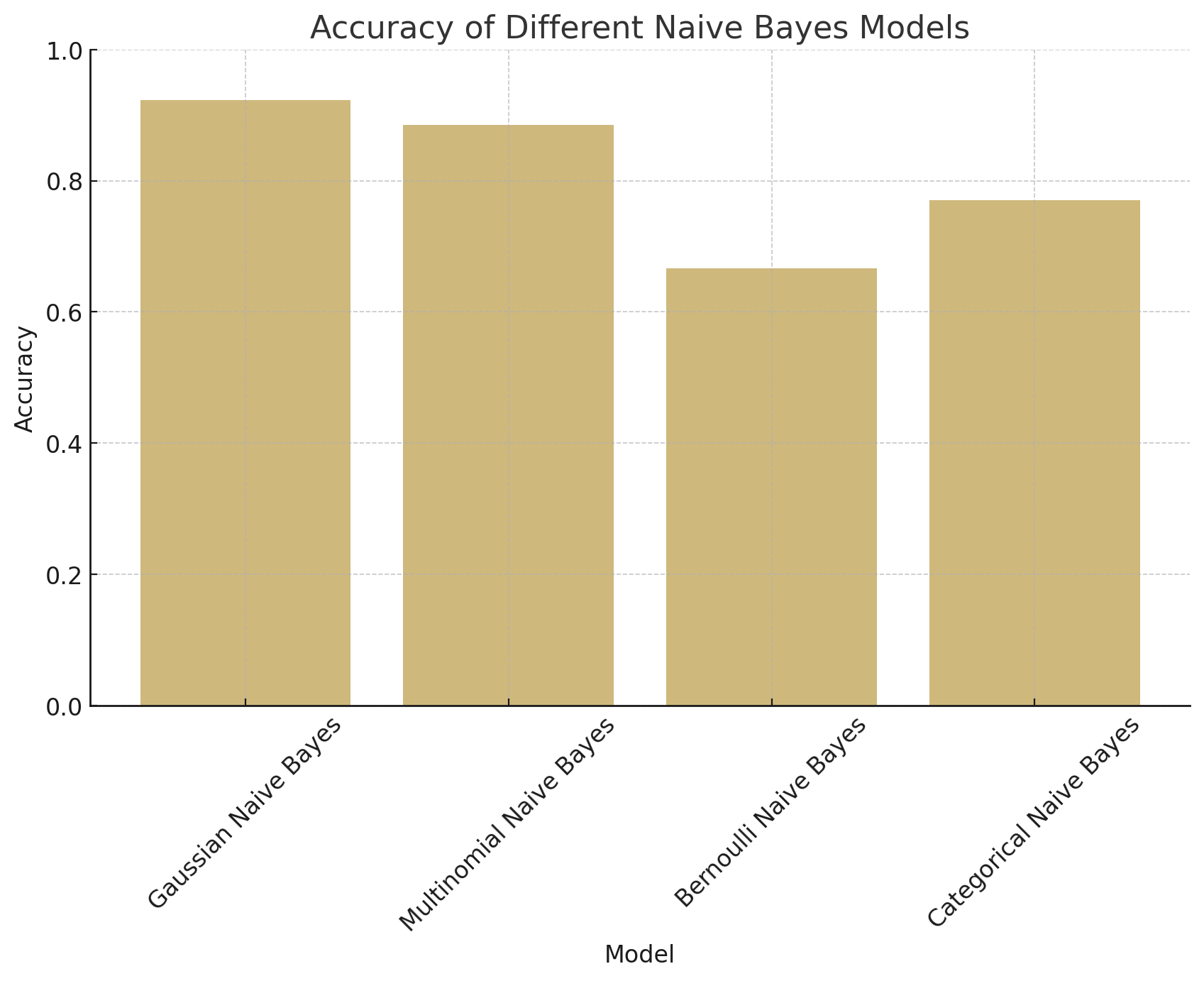
Conclusions

Based on the confusion matrices of the four Naive Bayes classifiers—Gaussian, Multinomial, Bernoulli, and Categorical—distinct differences in model performance are evident. The Gaussian Naive Bayes classifier showed the highest accuracy (92.3%), with a low number of false positives (11) and moderate false negatives (35), indicating a strong overall performance with the standardized continuous data. The Multinomial Naive Bayes, applied to discretized data, followed with an accuracy of 88.5%, showing a slightly higher count of both false positives (30) and false negatives (39), suggesting it is also effective but less robust in distinguishing between classes compared to Gaussian. The Bernoulli Naive Bayes classifier, which operates on binarized data, presented a lower accuracy of 66.7%, with a high number of false positives (199), pointing to significant challenges in differentiating between classes, likely due to data loss from binarization. Lastly, the Categorical Naive Bayes model achieved 77% accuracy with one-hot encoded data, with a moderate distribution of misclassifications (91 false positives and 47 false negatives). These results indicate that the Gaussian Naive Bayes classifier performs best for this dataset, suggesting that the continuous data structure aligns well with Gaussian assumptions. The comparatively lower accuracies of the Bernoulli and Categorical models highlight the limitations of binarized and categorical transformations for this specific prediction task, which benefits from retaining continuous variable relationships. Overall, the performance of each model underscores the importance of selecting a Naive Bayes variant suited to the data’s inherent structure for optimal classification outcomes.